Day 44

Superposition Analysis 

What is Superposition Theorem?

The Superposition Theorem is used to solve complex networks with a number of energy sources. It is an important concept to determine voltage and current across the elements by calculating the effect of each source individually. And combine the effect of all sources to get the actual voltage and current of the circuit element.

Superposition theorem states that;

“In any linear bilateral network having a greater number of sources, the response (voltage and current) in any element is equal to the summation of all responses caused by individual source acting alone. While other sources are eliminated from the circuit.”

In other words, we will consider only one independent source acting at a time. So, we need to remove other sources. The voltage sources are short-circuited and the current sources are open-circuited for ideal sources. If the internal resistance of sources is given, you need to consider the circuit.

The superposition theorem is only applied to the circuit which follows Ohm’s law.

When to Use the Superposition Theorem?

The network must follow the below requirements to apply the superposition theorem.

• The components used in the circuit must be linear. It means, for resistors, the flow of current is proportional to the voltage; for inductors, the flux linkage is proportional to current. Therefore, the resistor, inductor, and capacitor are linear elements. But the diode, transistor is not a linear element.
• The circuit components must be bilateral elements. It means, the magnitude of the current is independent of the polarity of energy sources.
• With the help of the superposition theorem, we can find the current passes through an element, voltage-drop of resistance, and node voltage. But we cannot find the power dissipated from the element.

• Related Post: Norton’s Theorem. Step by Step Guide with Solved Example

Steps to Follow for Superposition Theorem

Step-1 Find out a number of independent sources available in the network.

Step-2 Choose any one source and eliminate all other sources. If the network consists of any dependent source, you cannot eliminate it. It remains as it is throughout the calculation.

If you have considered all energy sources are ideal sources, you need not consider internal resistance. And directly short-circuit voltage source and open-circuit current source. But in case, if internal resistance of sources is given, you have to replace internal resistance.

Step-3 Now, in a circuit, only one independent energy source is present. You need to find a response with only one energy source in the circuit.

Step-4 Repeat step-2 and 3 for all energy sources available in the network. If there are three independent sources, you need to repeat these steps three times. And every time you get some value of the response.

Step-5 Now, combine all responses by algebraic summation obtained by individual sources. And you will get a final value of response for a particular element of a network. If you need to find a response for other elements, you need to follows these steps again for that element.

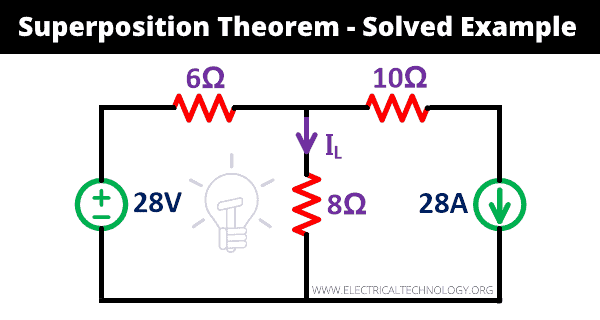
Superposition Theorem Solved Example

Example:

Let’s understand the working of the superposition theorem by example. Find the current (IL) passes through the 8Ω resister in the given network using the superposition theorem.

Solution:

Step-1 As shown in the above network, one voltage source, and one current source is given. Therefore, we need to repeat the procedure two times.

Step-2 First we consider 28V voltage source is present in the network. So, you need to remove the current source by open-circuited terminals. As here, we consider the current source as an ideal current source. So, we need not connect the internal resistance.

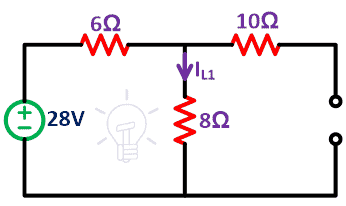
The remaining circuit is as shown in the below figure.

• Save to Pinterest

Step-3 Find the current (IL1) passes through 8Ω resister. It gives the effect only of a voltage source.

Due to the open circuit of a current source, no current passes through the 10Ω resister. So, the network consists of only one loop.

Apply KVL to the loop;

28 = 6IL1 + 8IL1

28 = 14IL1

IL1 = 28/14