My Study In Computer science : Day 22

Hallo every body today I will speak about Electric Potential

This tutorial is all about the energy associated with electrical interactions. Every time you turn on a light or use an electronic device, you are using electrical energy, an indispensable component of our technological society. Using work and energy concepts makes it easier to solve a variety of problems in electricity. In circuits, a difference in potential from one point to another is often called voltage. Potential and voltage are crucial to understanding how electric circuits work and have equally important applications in many devices.

Electric Potential Energy

Electric field exerts force on a charged particle ( $F = qE$ ) which can do work. This work can be expressed in terms of electric potential energy which is dependent on the position of the charged particle in the electric field; just as gravitational potential energy depends on the distance of a mass from the earth’s surface.

When a force $\overrightarrow{F}$ acts on a particle that moves from point a to

point b, the work done by the force is given by

where $dl$ is an infinitesimal displacement along the particle’s path and $\o$ is the angle between $\overrightarrow{F}$ and $dl$ at each point along the path. If $\overrightarrow{F}$ is conservative, the work done by $\overrightarrow{F}$ can be expressed in terms of potential energy $U$ . When the particle moves from a point where the potential energy is $U_{a}$ to a point where it is $U_{b}$ , the change in potential energy is $\Delta U = U_{b} - U_{a}$ and the work done by the force is

$W_{a \rightarrow b} = U_{a} - U_{b} = -\Delta U$

(2)

$U_{a}$ is the potential energy at the initial position and $U_{b}$ is the potential energy at final position. When $U_{a}$ is greater than $U_{b}$ , the force does positive work on the particle as it “falls” from a point of higher potential energy (a) to a point of lower potential energy (b); the potential energy decreases. When a tossed ball is moving upward, the gravitational force does negative work during the ascent as the potential energy increases. When the ball starts falling, gravity does positive work, and the potential energy decreases. The force does positive work if the net displacement of the particle is in the same direction as the force.

Electric Potential Energy in a Uniform Field

For an electric field that exerts a force $\overrightarrow{F} = qE$ ,

$W_{a \rightarrow b} = Fd = qEd$

(3)

Consider a positive test charge $q_{0}$ moving in a uniform electric field.

pos charge moving in and moving opposite

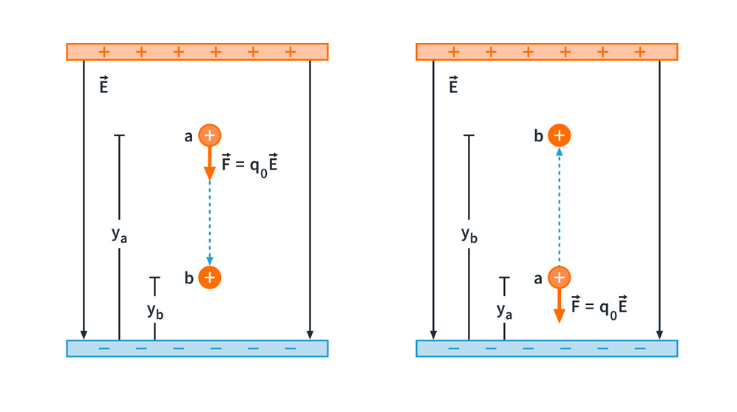
Figure 1: A positive charge moving (a) in the direction of $\overrightarrow{E}$ and (b) in the direction opposite $\overrightarrow{E}$

For Fig.1 (a), the field does positive work on the test charge because the force (pointing down) is in the same direction as the net displacement of the test charge. Since $W_{a \rightarrow b} = - \Delta U$ , if the work is positive then the potential energy ( $U$ ) decreases. For Fig.1 (b), the field does negative work on the charge and the potential energy increases.

Consider a negative test charge $q_{0}$ moving in a uniform electric field. Recall that when $q$ is negative, the force is opposite the field direction.

Negative charge moving in and the opposite

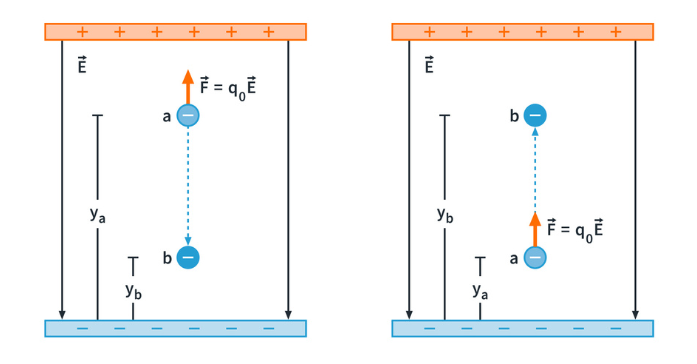
Figure 2: A negative charge moving (a) in the direction of $\overrightarrow{E}$ and (b) in the direction opposite $\overrightarrow{E}$

For Fig.2 (a), the work is negative since the force (pointing upward) is in the opposite direction as the net displacement of the negative test charge and the potential energy increases. For Fig.2 (b), the work is positive, and the potential energy decreases.

This shows us that whether the test charge is positive or negative, the following general rules apply:

$U$ decreases if $q_{0}$ moves in the same direction as the electric force $\overrightarrow{F} = q_{0} E$
$U$ increases if $q_{0}$ moves in the opposite direction as the electric force $\overrightarrow{F} = q_{0} E$

This is the same behavior as for gravitational potential energy, which increases if a mass m moves upward (opposite the direction of the gravitational force $\overrightarrow{F}_{g}$ ) and decreases if m moves downward (in the direction of $\overrightarrow{F}_{g}$ ).

When $U$ increases: An alternative but equivalent viewpoint is to consider how much work we would have to do to “raise” a particle from a point b where the potential energy is $U_{b}$ to a point a where it has a greater value $U_{a}$ (pushing two positive charges closer together, for example). To move the particle, we need to exert an additional external force $\overrightarrow{F}_{ext}$ that is equal and opposite to the electric-field force and does positive work. Therefore, the potential energy difference $U_{a} - U_{b}$ is the work that must be done by an external force to move the particle from b to a, overcoming the electric force. This viewpoint also works if $U_{a}$ is less than $U_{b}$ ; an example is moving two positive charges away from each other. In this case, $U_{a} - U_{b}$ is still equal to the work done by the force, but now the work is negative.

Electric Potential Energy of Point Charges

The idea of electric potential energy isn’t restricted to a uniform electric field. We can apply this concept to a point charge in any electric field caused by a static charge distribution. Recall that we can represent any charge distribution as a collection of point charges. It is therefore useful to calculate the work done on one test charge $q_{0}$ moving in the field caused by a stationary point charge $q$ .

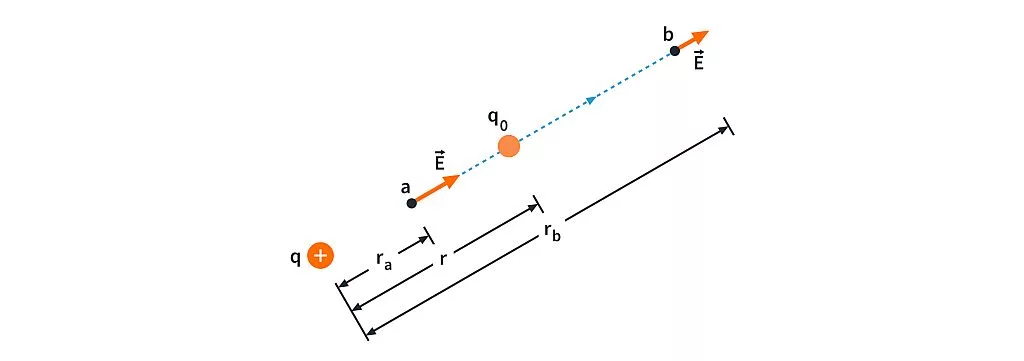
Figure 3: Test charge $q_{0}$ moves from a to b along a straight line extending radially from charge $q$ .

Note that the work done on $q_{0}$ by the electric field of $q$ does not depend on the path taken, but only on the distances $r_{a}$ and $r_{b}$ .

The force on $q_{0}$ is given by Coulomb’s law,

$\setcounter{equation}{3} \begin{equation}\groupequation{ \begin{split} F_{r} = \frac{1}{4\pi \epsilon _{0}} \frac{qq_{0}}{r^{2}} \end{split} }\end{equation} \end{document}$

If $q$ and $q_{0}$ have the same sign, the force is repulsive while if they have opposite signs, the force is attractive. The force is not constant during the displacement, and we must integrate to calculate the work Wab done on $q_{0}$ by Fr as $q_{0}$ moves from a to b:

$\setcounter{equation}{4} \begin{equation}\groupequation{ \begin{split} W_{a \rightarrow b} & = \int_{r_{a}}^{r_{b}} F_{r} \hspace{0.1cm} dr = \int_{r_{a}}^{r_{b}} \frac{1}{4\pi \epsilon _{0}} \frac{qq_{0}}{r^{2}} \hspace{0.1cm} dr \\ & = \frac{qq_{0}}{4\pi \epsilon _{0}} \left ( \frac{1}{r_{a}} -\frac{1}{r_{b}}\right ) \end{split} }\end{equation} \end{document}$

This is also valid for general displacements a to b that do not lie on the same radial line. The work done depends only on $r_{a}$ and $r_{b}$ , not on the details of the path. If $q_{0}$ returns to its starting point a by a different path, the total work done is zero. These are the qualities of a conservative force. Thus, the force on $q_{0}$ is a conservative force.

The result of the integral is consistent with $W_{a \rightarrow b} = U_{a} - U_{b} = - \Delta U$ if we define the potential energy at a and b to be

$U_{a} = qq_{0} / 4\pi \epsilon _{0} r_{a}$ when $q_{0}$ is a distance $r_{a}$ from $q$
$U_{b} = qq_{0} / 4 \pi \epsilon _{0} r_{b}$ when $q_{0}$ is a distance $r_{b}$ from $q$

Thus, the electric potential energy of two point charges is

$\setcounter{equation}{5} \begin{equation}\groupequation{ \begin{split} U = \frac{1}{4\pi \epsilon _{0}} \frac{qq_{0}}{r} \end{split} }\end{equation} \end{document}$

where $r$ is the distance between the two charges. The potential energy is positive if the charges have the same sign and negative if they have opposite signs.

Potential energy is defined relative to a chosen reference point where $U = 0$ is assigned. In eq.(6), $U$ is zero when $q$ and $q_{0}$ are infinitely far apart ( $r = \infty$ ). Therefore $U$ represents the work that would be done on the test charge $q_{0}$ by the field of $q$ if $q_{0}$ moved from an initial distance r to infinity. If $q$ and $q_{0}$ have the same sign, the interaction is repulsive in that they will repel each other, the work is positive, and $U$ is positive at any finite separation. As r approaches infinity, $U$ decreases and approaches zero. If $q$ and $q_{0}$ have opposite signs, the interaction is attractive, the work done is negative, and $U$ is negative. As r approaches infinity, $U$ increases and approaches zero.

We emphasize that the potential energy $U$ given by eq.(6) is a shared property of the two charges. If the distance between $q$ and $q_{0}$ is changed from $r_{a}$ to $r_{b}$ , the change in potential energy is the same whether $q$ is held fixed and $q_{0}$ is moved or $q_{0}$ is held fixed and $q$ is moved. For this reason, we never use the phrase “the electric potential energy of a point charge.” Likewise, if a mass m is at a height h above the earth’s surface, the gravitational potential energy is a shared property of the mass m and the earth.

Suppose the electric field in which the charge $q_{0}$ moves is caused by several point charges $q_{1}$ , $q_{2}$ , $q_{3}$ , ... at distances $r_{1}$ , $r_{2}$ , $r_{3}$ from $q_{0}$ .

Potential energy distance dependence

My Study In Computer science

الأربعاء، 30 أكتوبر 2024

Day 22

Electric Potential Energy

Electric Potential Energy in a Uniform Field

Electric Potential Energy of Point Charges

هناك تعليق واحد:

Day45

بحث هذه المدونة الإلكترونية