Hallo every body today I will speak about Electric Potential
This tutorial is all about the energy associated with electrical interactions. Every time you turn on a light or use an electronic device, you are using electrical energy, an indispensable component of our technological society. Using work and energy concepts makes it easier to solve a variety of problems in electricity. In circuits, a difference in potential from one point to another is often called voltage. Potential and voltage are crucial to understanding how electric circuits work and have equally important applications in many devices.
Electric Potential Energy
Electric field exerts force on a charged particle ( ) which can do work. This work can be expressed in terms of electric potential energy which is dependent on the position of the charged particle in the electric field; just as gravitational potential energy depends on the distance of a mass from the earth’s surface.
) which can do work. This work can be expressed in terms of electric potential energy which is dependent on the position of the charged particle in the electric field; just as gravitational potential energy depends on the distance of a mass from the earth’s surface.
When a force  acts on a particle that moves from point a to
acts on a particle that moves from point a to
point b, the work done by the force is given by

Electric Potential Energy in a Uniform Field
For an electric field that exerts a force  ,
,

(3)
Consider a positive test charge  moving in a uniform electric field.
moving in a uniform electric field.
Figure 1: A positive charge moving (a) in the direction of  and (b) in the direction opposite
and (b) in the direction opposite 
Figure 2: A negative charge moving (a) in the direction of  and (b) in the direction opposite
and (b) in the direction opposite 
For Fig.2 (a), the work is negative since the force (pointing upward) is in the opposite direction as the net displacement of the negative test charge and the potential energy increases. For Fig.2 (b), the work is positive, and the potential energy decreases.
This shows us that whether the test charge is positive or negative, the following general rules apply:
 decreases if
decreases if  moves in the same direction as the electric force
moves in the same direction as the electric force 
 increases if
increases if  moves in the opposite direction as the electric force
moves in the opposite direction as the electric force 
This is the same behavior as for gravitational potential energy, which increases if a mass m moves upward (opposite the direction of the gravitational force  ) and decreases if m moves downward (in the direction of
) and decreases if m moves downward (in the direction of  ).
).
When  increases: An alternative but equivalent viewpoint is to consider how much work we would have to do to “raise” a particle from a point b where the potential energy is
increases: An alternative but equivalent viewpoint is to consider how much work we would have to do to “raise” a particle from a point b where the potential energy is  to a point a where it has a greater value
to a point a where it has a greater value  (pushing two positive charges closer together, for example). To move the particle, we need to exert an additional external force
(pushing two positive charges closer together, for example). To move the particle, we need to exert an additional external force  that is equal and opposite to the electric-field force and does positive work. Therefore, the potential energy difference
that is equal and opposite to the electric-field force and does positive work. Therefore, the potential energy difference  is the work that must be done by an external force to move the particle from b to a, overcoming the electric force. This viewpoint also works if
is the work that must be done by an external force to move the particle from b to a, overcoming the electric force. This viewpoint also works if  is less than
is less than  ; an example is moving two positive charges away from each other. In this case,
; an example is moving two positive charges away from each other. In this case,  is still equal to the work done by the force, but now the work is negative.
is still equal to the work done by the force, but now the work is negative.
Electric Potential Energy of Point Charges
The idea of electric potential energy isn’t restricted to a uniform electric field. We can apply this concept to a point charge in any electric field caused by a static charge distribution. Recall that we can represent any charge distribution as a collection of point charges. It is therefore useful to calculate the work done on one test charge  moving in the field caused by a stationary point charge
moving in the field caused by a stationary point charge  .
.
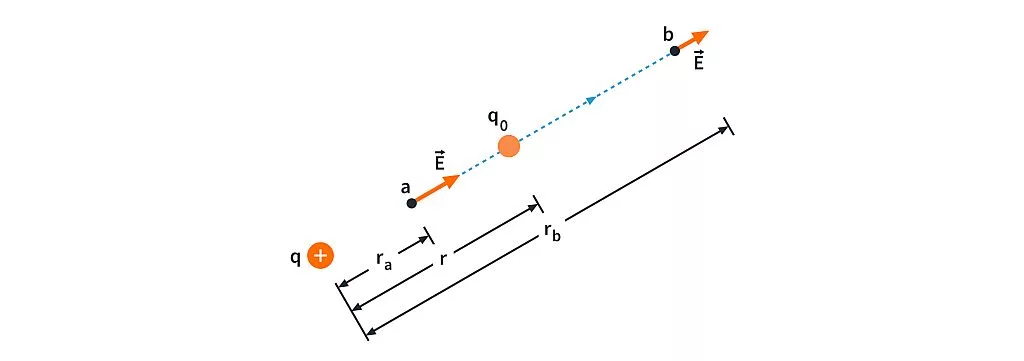
Figure 3: Test charge  moves from a to b along a straight line extending radially from charge
moves from a to b along a straight line extending radially from charge  .
.
where  is the distance between the two charges. The potential energy is positive if the charges have the same sign and negative if they have opposite signs.
is the distance between the two charges. The potential energy is positive if the charges have the same sign and negative if they have opposite signs.
Potential energy is defined relative to a chosen reference point where  is assigned. In eq.(6),
is assigned. In eq.(6),  is zero when
is zero when  and
and  are infinitely far apart (
are infinitely far apart ( ). Therefore
). Therefore  represents the work that would be done on the test charge
represents the work that would be done on the test charge  by the field of
by the field of  if
if  moved from an initial distance r to infinity. If
moved from an initial distance r to infinity. If  and
and  have the same sign, the interaction is repulsive in that they will repel each other, the work is positive, and
have the same sign, the interaction is repulsive in that they will repel each other, the work is positive, and  is positive at any finite separation. As r approaches infinity,
is positive at any finite separation. As r approaches infinity,  decreases and approaches zero. If
decreases and approaches zero. If  and
and  have opposite signs, the interaction is attractive, the work done is negative, and
have opposite signs, the interaction is attractive, the work done is negative, and  is negative. As r approaches infinity,
is negative. As r approaches infinity,  increases and approaches zero.
increases and approaches zero.
We emphasize that the potential energy  given by eq.(6) is a shared property of the two charges. If the distance between
given by eq.(6) is a shared property of the two charges. If the distance between  and
and  is changed from
is changed from  to
to  , the change in potential energy is the same whether
, the change in potential energy is the same whether  is held fixed and
is held fixed and  is moved or
is moved or  is held fixed and
is held fixed and  is moved. For this reason, we never use the phrase “the electric potential energy of a point charge.” Likewise, if a mass m is at a height h above the earth’s surface, the gravitational potential energy is a shared property of the mass m and the earth.
is moved. For this reason, we never use the phrase “the electric potential energy of a point charge.” Likewise, if a mass m is at a height h above the earth’s surface, the gravitational potential energy is a shared property of the mass m and the earth.
Suppose the electric field in which the charge  moves is caused by several point charges
moves is caused by several point charges  ,
,  ,
,  , ... at distances
, ... at distances  ,
,  ,
,  from
from  .
.




 ) which can do work. This work can be expressed in terms of electric potential energy which is dependent on the position of the charged particle in the electric field; just as gravitational potential energy depends on the distance of a mass from the earth’s surface.
) which can do work. This work can be expressed in terms of electric potential energy which is dependent on the position of the charged particle in the electric field; just as gravitational potential energy depends on the distance of a mass from the earth’s surface. acts on a particle that moves from point a to
acts on a particle that moves from point a to  is an infinitesimal displacement along the particle’s path and
is an infinitesimal displacement along the particle’s path and  is the angle between
is the angle between  and
and  . When the particle moves from a point where the potential energy is
. When the particle moves from a point where the potential energy is  to a point where it is
to a point where it is  , the change in potential energy is
, the change in potential energy is  and the work done by the force is
and the work done by the force is
 ,
,
 moving in a uniform electric field.
moving in a uniform electric field.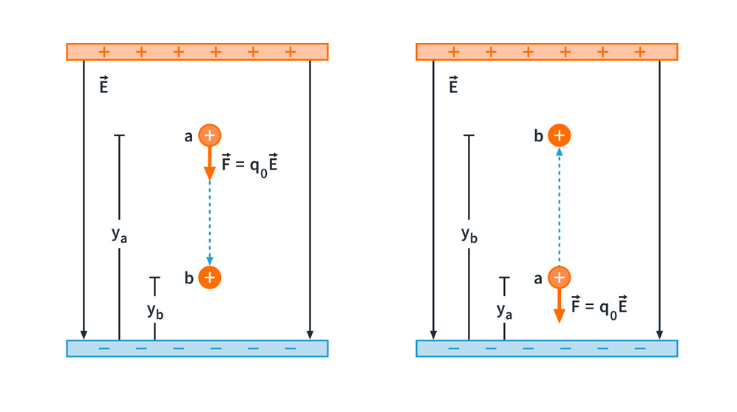
 and (b) in the direction opposite
and (b) in the direction opposite  , if the work is positive then the potential energy (
, if the work is positive then the potential energy (  ) decreases. For Fig.1 (b), the field does negative work on the charge and the potential energy increases.
) decreases. For Fig.1 (b), the field does negative work on the charge and the potential energy increases. moving in a uniform electric field. Recall that when
moving in a uniform electric field. Recall that when  is negative, the force is opposite the field direction.
is negative, the force is opposite the field direction.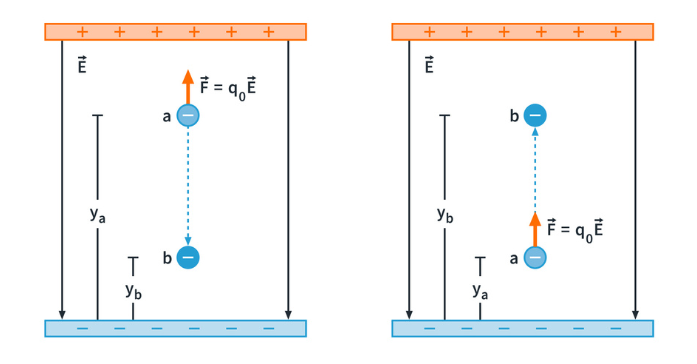
 and (b) in the direction opposite
and (b) in the direction opposite 
 ) and decreases if m moves downward (in the direction of
) and decreases if m moves downward (in the direction of  that is equal and opposite to the electric-field force and does positive work. Therefore, the potential energy difference
that is equal and opposite to the electric-field force and does positive work. Therefore, the potential energy difference  is the work that must be done by an external force to move the particle from b to a, overcoming the electric force. This viewpoint also works if
is the work that must be done by an external force to move the particle from b to a, overcoming the electric force. This viewpoint also works if  .
.
 and
and  .
.

 if we define the potential energy at a and b to be
if we define the potential energy at a and b to be when
when  when
when 
 is the distance between the two charges. The potential energy is positive if the charges have the same sign and negative if they have opposite signs.
is the distance between the two charges. The potential energy is positive if the charges have the same sign and negative if they have opposite signs. is assigned. In eq.(6),
is assigned. In eq.(6),  ). Therefore
). Therefore  ,
,  ,
,  , ... at distances
, ... at distances  ,
,  ,
,  from
from 

